
Calculations:
Mass(m): 0.2 [kg]
Wheel radius(r): 0.040952[m]
Gravity(g): 9.8 [m/s2]
Torque = r x m x g = (0.040952)*(0.2)*(9.81) = 0.080348 [Nm]
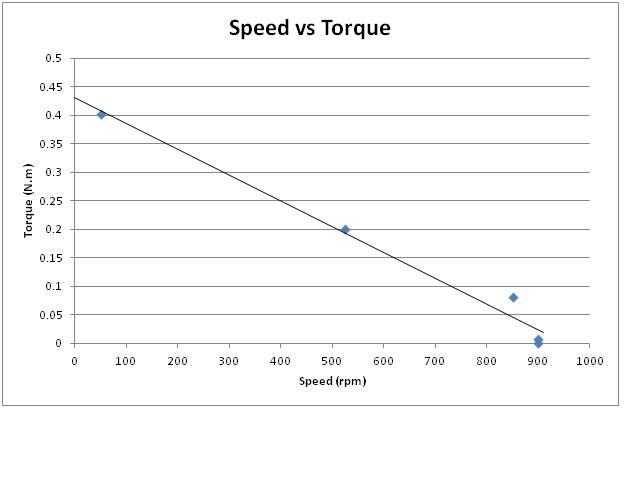
Similarly, the torque was determined for the mass of .4 kg, .8 kg and 1 kg which is summarized in the table 1 underneath.
Table 1: Summary for the torque at different loads.
| Mass (kg) | Speed (rpm) | Torque (N.m) |
| 0 | 900 | 0 |
| 0.02 | 900 | 0.008035 |
| 0.2 | 850 | 0.080348 |
| 0.5 | 525 | 0.20087 |
| 1 | 50 | 0.401739 |
*: The speed was obtained by , where Ѳ represents the angular speed of the motor caused by the load.
Rise time: 14(counts) *10ms (time interval between every count) Rise time = .14 sec
Time constant: tr = 2.2*Т 0when rise time ranges from 10-90%. Т = .0636 sec
Table 2: Data
| Mass (kg) | Angular speed ( | u (V) | I (A) |
| .020 | 900 | 8.16 | .25 |
Sample calculations to obtain mechanical power, electrical power and inertia.
τ = .020*9.80*.040952 τ = .008026592 N.m
PMech = τ *ωm PMech = PMech = 0.7565 W
PElec = u*I PElec = 8.16 W*.25 A PElec = 2.04 W
η = η = η = 0.3708
Ke (electric constant) = Ke = Ke = .0866
Kt (Torque constant) = η*Ke Kt = 0.3708*.0866 Kt = .0321
Moment of Inertia: τs =
In order to calculate Ra, we need to determine the stall torque. Stall torque is the maximum torque which cant be exceeded by the motor power. From the graph, maximum torque happens when speed is equal to 0, therefore Тs = .435 N/m
Solving Ʈs when load of 1 kg was applied to the motor to obtain the approximate idea of the maximum mass which can be attached and controlled by the motor without reaching stall torque.
τ = τs (1 - ) τs = τs = τs = 0.4249 N.m
τs = 0.435 = Ra = 0.053 Ω
Moment of Inertia: τs = J = J = 0.00335kg.m2.
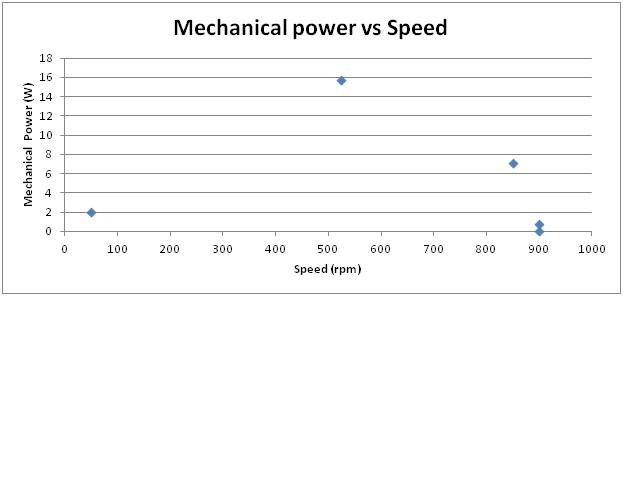
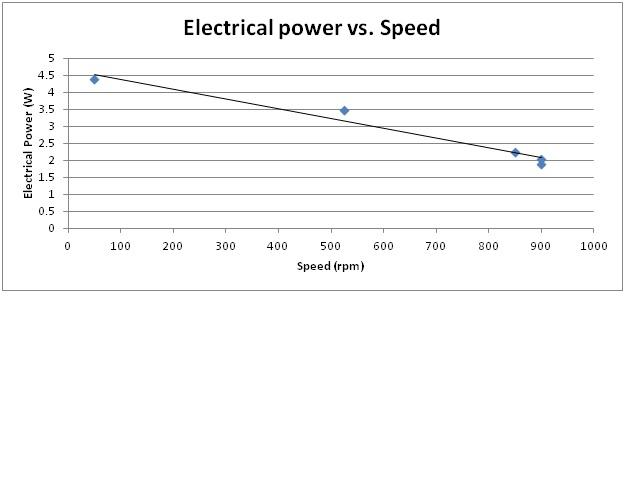
Similarly, the electrical power and mechanical power was calculated for different loads whose results are summarized in table underneath.
Table 3: Summary of mechanical and electrical power with respect to mass.
| Mass (kg) | P(mech) (W)
| P(elec) (W) |
| 0 | 0 | 1.8791 |
| 0.02 | .7565 | 2.04 |
| 0.2 | 7.1446 | 3.12 |
| 0.5 | 15.7602 | 3.48 |
| 1 | 2.101 | 4.38 |